12tones

Twelve Tone Melodies

s a composer of Twelve-Tone Melodies, you realize that there are exactly twelve choices for the first note in your tone row, the 13th tone of the chromatic scale necessarily being a repetition of some other tone. That leaves 11 tones from which to choose for the second note, 10 for the third, and so forth, until you run out of tones.

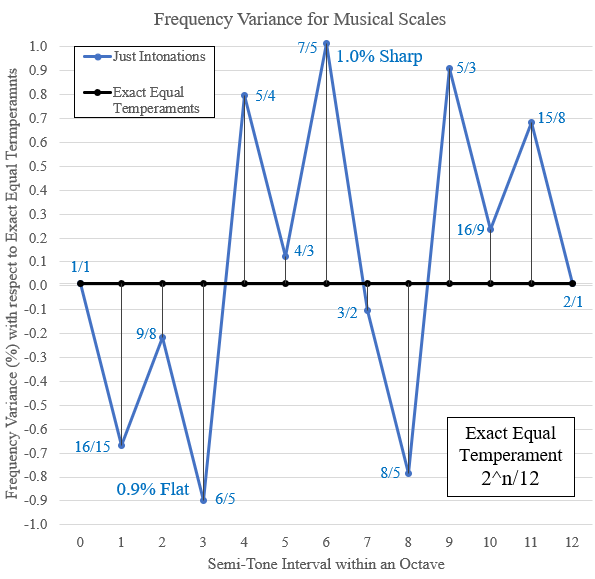
If you have solved the Factorial Factoid puzzle, you realize [a] that if dodecaphony imposes a limit on the number of possible Twelve-Tone Melodies, there must be total of only 12! permutations of chromatic notes without repetitions and [b] that the previous exclamation point is not being used for emphasis!

Using your calculator, you quickly multiply 12, 11, 10, 9, 8, 7, 6, 5, 4, 3, 2, 1 and get...

12! = 479,001,600 possible Twelve-Tone Melodies

...which is, nevertheless, quite a large number. A little more calculating and you determine that composing the full repertoire of Twelve-Tone Melodies at the brisk rate of one new tune per minute would take more than 911 years, working 3.428571 (= 24 / 7, get it?).

An exclamation point here will be reserved for denoting factorials -- and for the discovery of a mistake!

Consider...

A melody starting at a given note can be moved as a whole up or down the musical scale so that it starts at some other note. That's called "transposition." The melody stays the same. All the notes are thus relative to each other, and the selection of the first note defines 12 identical melodies. So we must divide 479,001,600 by 12 for our solution or else re-calculate as follows:

11! = 39,916,800 possible Twelve-Tone Melodies

...which cuts our production time for the whole repertoire to about 76 years.

Nota Bene: A lot depends on what scale is being used. For example, one scheme is called "Just Intonation." It applies ratios of integers to the sound frequencies...

1/1, 16/15, 9/8, 6/5, 5/4, 4/3, 7/5, 3/2, 8/5, 5/3, 16/9, 15/8, 2/1

As mathematically polite as integers may be, the resulting intervals between successive notes in an octave will be slightly unequal to each other, such that various transpositions will sound different...

If you want all transpositions to produce the same melody, then you would use the "Exact Tone Equal Temperament" scale, which applies multiples of (ugh) the twelfth root of two...

1, 2^1/12, 2^1/6, 2^1/4, 2^1/3, 2^5/12, 2^1/2, 2^7/12, 2^2/3, 2^3/4, 2^5/6, 2^11/12, 2

Musicians will not agree with this solution, of course. There is more to a melody than just the sequence of its notes. Varying the duration of each note or inserting rests between notes would seem to expand the number of Twelve-Tone Melodies indefinitely.

ell, not quite indefinitely. Consider varying the duration of each note using five of the most common fractions: whole-note, three-quarter-note, half-note, quarter-note, eighth-note. Each tone would then be followed by a rest of any of the five durations available for notes -- plus duration 0 (no rest).

We have, then, 5 + 5 + 1 = 11 temporal characteristics for each note. Let's add a second rest-state, for indicating a continuous slide from a given tone to its immediate successor, bringing the total alternative melodies to twelve.

Thus, the quantity of Twelve-Tone Melodies = 12 times 11! = 12!! The second exclamation point in the previous sentence is for emphasis.

Home Page Puzzle Page Logic and Reasonings The Puzzle as a Literary Genre