 f
course, you recognized at once that the wager
is an elementary exercise in probability theory, and you remembered the
solution: That, given as few as 23 persons selected at random, there is
a better than an even chance that at least two of them have the same birthday
{HyperNote}.
Both you and the statistician were able to count only
20 persons, so it was not an even bet. Based on numbers, you would likely
lose -- a situation made decidedly worse by the evidence of a birthday
being celebrated at the nearby table, unless..., unless...
You would expect that, even while losing her own bet, your
friend might have wished you a happy birthday.
HyperNote
 he
solution is traditionally found by first reversing the statement of the
problem:
Instead of asking...
Selecting at random, how many people are needed to assure
an even bet that at least two of them share the same birthday?
...the sophisticated solver asks...
Selecting at random, how many people are needed to assure
an even bet that no two of them share the same birthday?
For convenience, let's let...
n = the unknown number of persons,
p = the probability that two or more persons share the
same birthday, and
q = the probability that no two persons share the same
birthday.
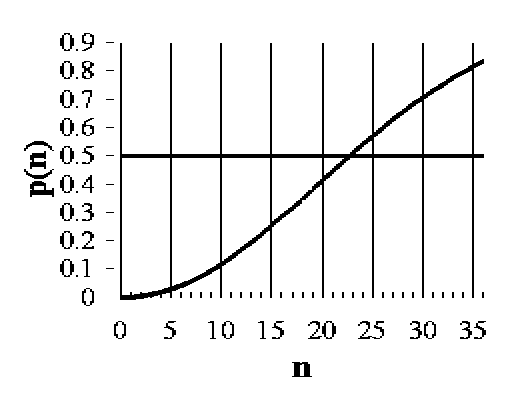
You seek the minimim value for n such that p > 1/2. You know
that p = 1 - q, and you can easily find the value of q for two extreme
values of n...
If n = 1, then q = 1 and p = 0 -- impossible: no other
person with whom to share a birthday.
If n = 365, then q = 0 and p = 1 -- certainty: no more
birthdays to spread around without duplicates.
For every value of n, there are 365n possible
combinations of birthdays, which is absolutely all there can be. Accordingly,
that is what goes into the denominator of the fraction used to calculate
your probability q. Your numerator requires only slightly more sophistication
in numbers.
Any person you might select at random will have one of
365 birthdays. That leaves only 364 birthdays for the second person, in
order to satisfy the part of the conditions mandated by probability q which
says "no two of them share the same birthday." Having given one of those
birthdays to the second person, you will have only 363 birthdays for the
third person. And so forth.
You can make a table and a graph as follows:
|
n
|
q
|
p
|
|
1
|
(365)
(365)
|
0
|
|
2
|
(365)(364)
(365)(365)
|
0.00274
|
|
3
|
(365)(364)(363)
(365)(365)(365)
|
0.00820
|
|
4
|
(365)(364)(363)(362)
(365)(365)(365)(365)
|
0.01636
|
|
...
|
and so forth
|
...
|
|
23
|
Hoo-ha!
|
0.507297
|
|
