ime-distance-velocity problems are all around us.  None having greater day-to-day practicality than the one posed in To Brake or Not to Brake.   On the right, you see a "phase-plane plot" , which depicts relationships between distance and velocity -- but not time.  Asking a "sooner or later" question calls for calculations in the time domain; nevertheless, the phase-plane plot is useful for correlating events in space.

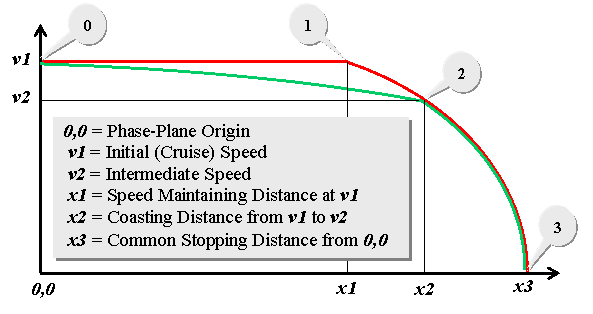Here a parabola represents a constant deceleration (see Trail Braking).  The red car can be seen delaying its deceleration to Point 1, a distance x1 feet, while the green car coasts to Point 2, a distance of x2 feet.  Point 2 marks the location in space where both cars pass through v2, albeit at different times.

As with other puzzles (see for example Jump in a Lake and Short Cut?) almost everything is unknown, inviting us to make assumptions.  For the Sooner Arrival part of the puzzle, however, let's try generalizing the unknowns over practical ranges and then create a mathematical model for exploring what might be called a whole "envelope of solutions."

little modeling music, please...

Let the distance ahead that the drivers observe the signal x3 be an independent variable ("foozling parameter" in the vernacular of mathematics).

The red car's stopping distance can be calculated as follows: x3 - x1 = v1²/ 2 dB, where dB is the braking deceleration.  Rearranging, we have...

x1 =  x3 - v1²/ (2 dB)

...which is the greatest distance the red car can travel at v1 before braking.

The phase-plane plot shows us that the two cars share Point 2 (though at different times).  This enables us to write two equations for x2...
 

1. x2 = x1 + (v1² - v2²) / 2dB
2. x2 = (v1² - v2²) / 2dC


...which uses dC to model coasting as a constant deceleration.  That assumption sets aside wind resistance at higher speeds.  In the phase-plane plot, a straight line gives a slightly closer approximation of reality than a parabola.  You might take your car out on a level road and determine reasonable values for dB and dC.

Algebraic manipulations give us the ability to express the value of v2 in terms of the other variables...

v2 = [v1² - 2dBdC x1 / (dB -dC)]^1/2

Now, for the time variables, we have...

tB1 = x1 / v1
tB2 = tB1 + (v1 - v2) / dB = x1 / v1 + (v1 - v2) / dB
tC2 = (v1 - v2) / dC
tB3 = tB1 + v1 / dB = x1 / v1 + v1 / dB
tC3 = tC2 + v2 / dB = (v1 - v2) / dC + v2 / dB

...which means the red car arrives sooner than the green car by...

Delta-t:  tC3 - tB3 = (v1 - v2) / dC + v2 / dB - [x1 / v1 + v1 / dB] seconds

Let: x3 = 1,000 feet, dB = 10 MPH/sec, dC = 1 MPH/sec,  v1 = 65 MPH

Oh right, and that only gets the red car to Point 3 sooner than the green car, not necessarily quicker to the destination.  Indeed, if the traffic signal continues to indicate a stop beyond tC3, the comparison starts all over again.

If the requirement to stop is imposed by congestion, side-by-side results will be about the same.  As you well know, in congested flow extremely low speeds are likely, so opportunities for coasting will be limited by the patience of the driver behind you and arrival at the destination will be limited by the presence of traffic ahead not by stoplights.

Later Refill

f you have shopped for a new car in recent times you are surely familiar with the mileage label displayed in the rear window on the right.  The figure for HIGHWAY MPG is usually about 1.3 times that for the CITY MPG: (in this case, 31/24 = 1.292).  Don't you wonder why?

The official EPA ratings are determined by empirical measurements made while driving a specimen vehicle on a dynamometer over two prescribed profiles.  The HIGHWAY run is conducted at high speeds, and the CITY run tests the vehicle's stop-and-go performance.

Nota bene: It is too generous to assume that the most salient effects are faithfully simulated.  Dynamometers may not precisely impose the effects of inertia and properly calibrate wind resistance.  Nevertheless, that's the way the EPA gets those numbers.

Meanwhile, CITY MPG, which is measured at low speed with a whole lot of stopping and going in the profile, must be impacted by something other than aerodynamic drag.  What might that be?

Here is a simplified diagram published by the EPA that depicts how energy in fuel gets consumed when a vehicle goes driving along on a level road.  The percentages represent overall averages -- referencing neither HIGHWAY's speed nor CITY's stop-and-go operations.  The diagram indicates that only 12.6% of what you pay for at the pump gets converted to mechanical energy delivered to the wheels.  The only good news in that diagram is embedded in the word inertia.  All the other numbers represents energy losses.

Sure, it is a fact that inertia must be overcome during acceleration ("A body at rest tends to remain at rest"), but once the vehicle is accelerated, inertia disappears ("A body in motion tends to remain in motion").  On a level road at a constant speed, none of the energy in fuel is being used to maintain inertia.  Same for coasting, by the way.  The previous two sentences could use exclamation points.

It is easy to see that braking is the culprit in limiting CITY MPG.  Braking means a loss of inertia -- a loss that must be replaced during the subsequent acceleration.   As shown in the diagram, on the average, braking consumes 5.8% of the energy in fuel; however, at low speed, braking dominates the past energy flow to inertia.  It's the 'stop' not the 'go' that wastes the energy.  Accordingly, if the vehicle could be operated without braking except for emergencies, CITY MPG ought to be at least comparable to HIGHWAY MPG (if not substantially better, considering the artifacts in dynamometry mentioned above).   In congested traffic flow, of course, that may not be practical, but it is clear that more coasting means more mileage.

A precise solution to the present puzzle calls for many assumptions about vehicle characteristics and the overall profile of postulated trips between fill-ups, including speeds and the number of starts and stops.  Instead, we might simply bracket the sooner and later numbers based on the reasoning above as follows:
 

Epilog: Message received from Dr. David Walker at NIST on September 1, 2006...
 

Nice work, Paul!

Evidence of the verity of your conclusions reside in the anecdotal case of the 2006 Toyota Prius hybrid, which has an EPA economy rating of 60/51 city/highway. That's right; the city mpg is higher than the highway mpg, for exactly the reasons you spell out. Ain't regenerative braking a wonderful thing? The Prius (along with most other hybrids) also benefits from significantly reduced losses when on standby/idling -- which comprises 17.2% of the total fuel consumption in the EPA diagram--since they shut off the engine whenever possible.

Cheers,
Dave

Thanks, Dave,  for your compliments and comments.

The benefits of the hybrid for CITY MPG are not entirely attributable to regenerative braking, which, unfortunately, does not live up to its hype.  The elementary sketch below depicts the flow of power delivered to/from the wheels for the cases posed in the To Brake or Not to Brake puzzle.  Negative values indicate potential regenerative power from braking. 

As a practical matter, though, not all of that power can be used to charge the hybrid's battery.  At slower speeds, for example, the voltage levels generated from braking will not exceed the battery float.  Then, too, when the vehicle is moving faster, the battery must be maintained in a "receptive" state, which means not fully charged, in anticipation of future brake applications. 

In reciprocity, when stopped and during standby/idling periods, the hybrid's battery must continuously supply accessory power, such as for lighting and air-conditioning.  That requirement mandates keeping the battery fully charged as much as possible, which deprives the system from the benefits of regenerative braking. 

Best regards,
Paul