| A train control system that is not designed to ascertain
the speed of trains must regard the train ahead as being stopped.
In railroading parlance, that is known as the... |
Brick Wall Assumption
 Conventional,
"fixed-block" train control systems might best be assumed for this
puzzle. Such a system is designed to detect trains in “track
circuits” by the "shunting" of their wheels. Each track circuit defines
a "block" of track, which can be hundreds or thousands of feet in length.
Changes in speed commands must be delivered from the "wayside" to a
train based on the location of its "lead car" ("cab signaling," it's called).
New speed commands are also received as the train moves from block to block
(see Confusion Free Codes). Conventional,
"fixed-block" train control systems might best be assumed for this
puzzle. Such a system is designed to detect trains in “track
circuits” by the "shunting" of their wheels. Each track circuit defines
a "block" of track, which can be hundreds or thousands of feet in length.
Changes in speed commands must be delivered from the "wayside" to a
train based on the location of its "lead car" ("cab signaling," it's called).
New speed commands are also received as the train moves from block to block
(see Confusion Free Codes).
At any given moment, the location of the train ahead is
determined by its "tail car," which is assumed to be situated at the rear-most
boundary of the track block in which it is detected. For safety,
it is also appropriate to assume that an impenetrable barrier is located
at that boundary -- and that the barrier will stay there until the train
ahead no longer occupies the block. Accordingly, as the preceding
train moves forward, the so-called "brick wall" gets torn down and immediately
re-built at the next block boundary, leaping logically from block to block.
Sketches like the one below apply what is known in mathematics
as a "phase-plane plot" -- a graph of velocity against displacement (in
this case, train speed versus track location).
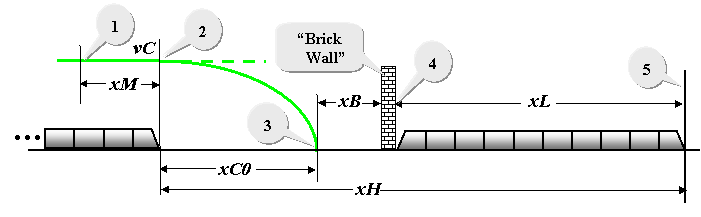 We see that the train control system, having detected the
train ahead, commands the "train-in-trail" to switch from propulsion to
“service braking” just as it reaches Point 1. That won't be accomplished
instantaneously. Instead, the train-in-trail must undergo a "mode
change delay" tM, during which it will cover a distance xM
traveling at vC and arriving at Point 2, where braking actually
begins. In a phase-plane plot, a constant deceleration appears as
a parabola, such that distance required to decelerate from vC
to a stop is given by...
We see that the train control system, having detected the
train ahead, commands the "train-in-trail" to switch from propulsion to
“service braking” just as it reaches Point 1. That won't be accomplished
instantaneously. Instead, the train-in-trail must undergo a "mode
change delay" tM, during which it will cover a distance xM
traveling at vC and arriving at Point 2, where braking actually
begins. In a phase-plane plot, a constant deceleration appears as
a parabola, such that distance required to decelerate from vC
to a stop is given by...
xC0 = vC2 / 2 dS
...where dS is a constant deceleration as
customarily modeled for "service braking." The train comes to a stop
at Point 3, which is deliberately targeted at a distance xB
in approach to the brick wall located at Point 4. The size of xB
is mostly attributable to the fixed-block design and represents a "buffer"
distance that allows for uncertainty in the stopped location of the train-in-trail.
 Keep
in mind that the train ahead is probably not stopped at all but
traveling down the track at, say, vC, with its tail car
at Point 5 or beyond. If so, the brick wall at Point 4 may actually
be torn down prior to the train-in-trail reaching Point 1, and no command
for
Trail Braking will be given. Trains
operating on their respective "time-table" schedules will generally stay
much farther apart, but if the train ahead is delayed, a minimum headway
distance
xH
must nevertheless be assured for "following move" separations. To
estimate the minimum headway
time tH
for trains operating
at vC, then, we calculate... Keep
in mind that the train ahead is probably not stopped at all but
traveling down the track at, say, vC, with its tail car
at Point 5 or beyond. If so, the brick wall at Point 4 may actually
be torn down prior to the train-in-trail reaching Point 1, and no command
for
Trail Braking will be given. Trains
operating on their respective "time-table" schedules will generally stay
much farther apart, but if the train ahead is delayed, a minimum headway
distance
xH
must nevertheless be assured for "following move" separations. To
estimate the minimum headway
time tH
for trains operating
at vC, then, we calculate...
tH = tM + [(vC2
/
2 dS) + xB] / vC.
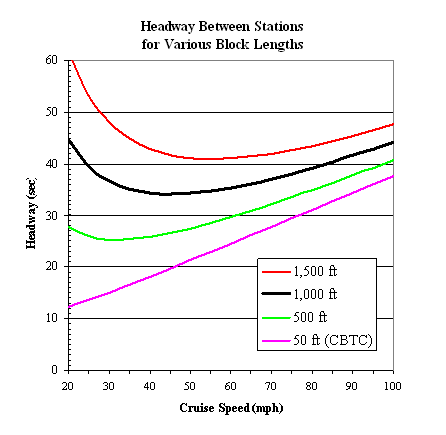
Solutions for the Trail Braking
puzzle are provided by the graph on the right using "base-case" values
as follows: train length xL = 700 feet, mode-change delay
tM
= 4 seconds, and service brake rate dS = 3 miles per hour
per second (mphps).
With xB = 1,000 feet,
the shortest headway
tH = 34 seconds at vC
< 50 miles per hour.
|
 Higher
cruise speeds are desirable, obviously, for they will improve trip-times
between stations, but higher speeds will also increase the minimum
headways between trains. That will seem counter-intuitive to some
readers. It may help to imagine driving a race-car in a video game
always approaching a brick wall that randomly jumps ahead the length of
a football field along the race-track. Higher
cruise speeds are desirable, obviously, for they will improve trip-times
between stations, but higher speeds will also increase the minimum
headways between trains. That will seem counter-intuitive to some
readers. It may help to imagine driving a race-car in a video game
always approaching a brick wall that randomly jumps ahead the length of
a football field along the race-track.
Meanwhile, the abbreviation "CBTC" in the graph legend
stands for Communications Based Train Control, an advanced system which
achieves the effect of extremely short block lengths -- as if the brick
wall gets torn down permanently. The result is called "moving-block"
train control. The graph shows that CBTC will support the same headway
(tH = 34 seconds) at cruise speeds over 90 miles per hour
-- a potential savings of more than 30 seconds per mile in trip-time.
By the way, even a fixed-block system can handle more than a train a minute
(tH = 60 seconds) at cruise speeds exceeding 100 miles per
hour.
Oh right, there is just this one other matter. Passengers.
And Station Stops. |
