|
Copyright ©2016 by Paul Niquette. All rights reserved.
Level flight
requires a balance of aerodynamic forces --
especially in pitch.
Stability requires that vertical perturbations
will be correctable by aerodynamic control
forces. Moreover, in the event of an
engine failure, the aircraft must not stall
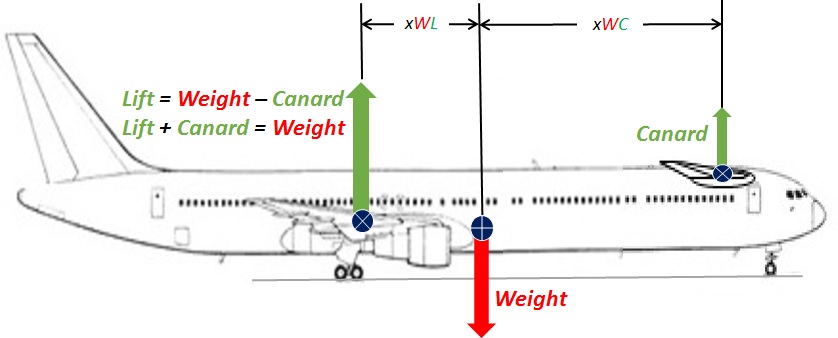
by default. That means the center
of gravity for an aircraft is
located forward of the center
of lift as shown in the
puzzle.
The resulting nose-heaviness
in level flight must be balanced either by a
downward force provided by the elevator
located in the empennage
or by an upward force provided by a
canard located near the nose of the
aircraft. In the Conventional
Configuration, the required forces obey the
following equation: Lift = Weight + Elevator.
For the Canard Configuration, the equation must be
changed to read Lift
= Weight - Canard.
Nota bene, elevator is a misleading term. It controls pitch. Same for the canard, by the way. Pitch determines the angle-of-attack between the wing and the relative wind. Thus either the elevator or the canard controls angle-of-attack. It is thrust that really controls the "elevating" of an aircraft, whether climbing, descending, or in level flight. Loss of thrust results in loss of altitude but must not result in an increase in angle-of-attack toward a stall condition. Thus, for safety, center of gravity must be located forward of center of lift.
Balancing forces, Elevator and Canard, are provided by air flowing over and under the respective control surfaces. The expression 'pitch authority' can be used to characterize the 'torques' on the fuselage resulting from those two forces. Torque is proportional to the product of the surface area of a control and its moment arm.Solvers are invited to use the sketch below, which depicts the respective moment arms for the aerodynamic forces in reference to the aircraft's center of gravity.... 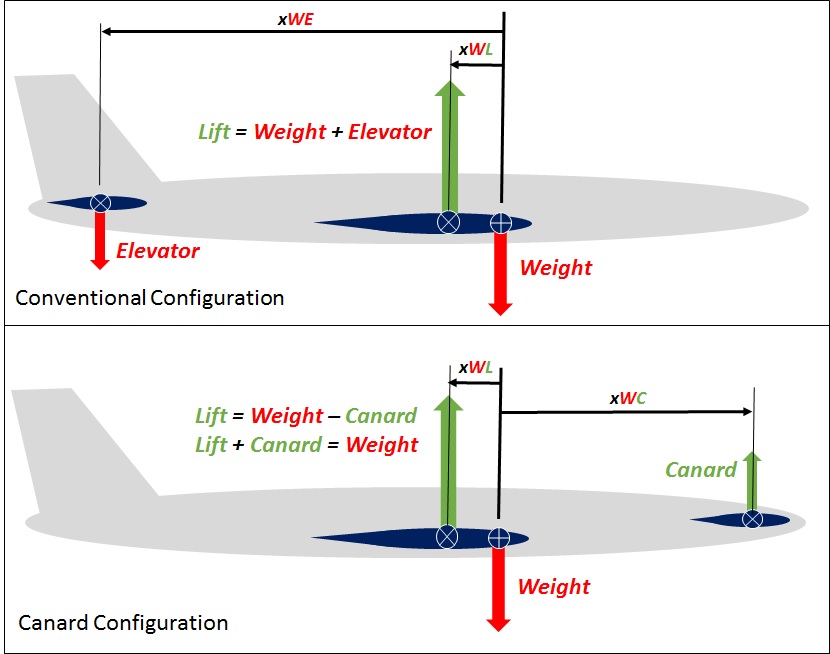 Sophisticated solvers might make the assumption that xWL is the same for the two configurations then calculate the balancing torques with respect to each aircraft's center of gravity for each configuration.
The ratio of the required balancing force on a canard compared to an elevator varies inversely with the length of their respective moment arms. Here are three interesting cases... Case 1. xWE = xWC, Canard = Elevator Case 2. xWE > xWC, Canard > Elevator Case 3. xWE < xWC, Canard < Elevator
In
all three
cases, there is
a Canard
Advantage
as derived
above.
Having the
largest
value for
Canard,
an
up-lifting
force,
Case 2 would
seem to offer
the greatest
reduction in
required Lift;
however, Case
2 requires
the largest
control area
and therefore
the highest
incremental
weight
for the canard
itself.
Solvers
of the Tin-Can Mystery puzzle will recall that surface
area of an
object varies
as the square
of a linear dimension,
while volume
and therefore
weight varies
as the
cube. One
can
estimate that
the weight
of the canard
varies
with surface
area according
as the
3/2-power, (Canard
/ Elevator)3/2.
Solvers who study the historical collection of canard aircraft listed in the puzzle will find configurations with a wide variety of moment arms and control surfaces.Let us conclude by analyzing the Boeing 767 canard configuration postulated in the puzzle. The sketch below applies the parameters defined above. The moment arm for the center of lift with respect to the center of gravity xWL is assumed to be the same for both configurations. 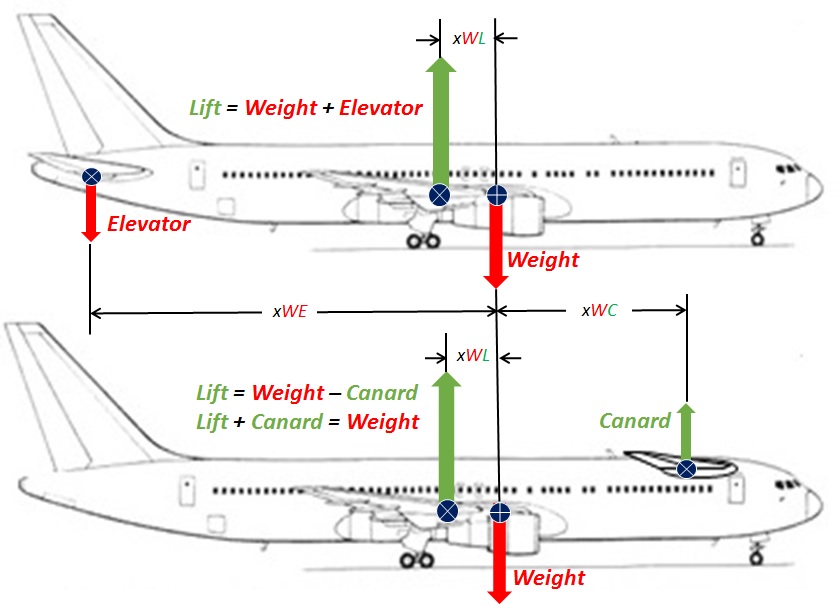
One might
estimate that the moment arm
for the Elevator
xWE to
be about twice
the moment arm
for the Canard
xWC,
which means the required
balancing
force Canard > Elevator by a factor
of two,
which
corresponds to Case
2. There
would be a penalty of about
83%
of the weight
of the
elevator
in
the Canard
Configuration,
which is small
compared
to the Canard Advantage
resulting
from the reduction of requisite Lift, which solvers will find described in Wages
of Flight.
Illustrated below is a postulated lengthening the fuselage for the Boeing 767, which exploits the Canard Advantage by applying the increase in useful load as accommodations for a larger number of passengers or space for freight...
Finally, the Canard Advantage includes a solution to the problem of ground effect under the elevator. During its take-off roll, the pilot of a fully loaded transport aircraft must perform a rotation maneuver at a specified speed V-R, lifting the plane's nose to increase the angle-of-attack on the wings for lift-off. In the Conventional Configuration that means the elevator is being brought low to the ground such that pressure increases underneath tending to prevent further rotation. If the pilot delays rotation until after accelerating to a higher speed, the aircraft may not be able to take off before the end of the runway. |