|
Copyright ©2004 by Paul Niquette. All rights reserved. |
|
Copyright ©2004 by Paul Niquette. All rights reserved. |
|
They cannot all be right. Let's get to work (if you don't dig trig, you can skip on down to here). Figure 1 depicts a horizontal view of an airplane in straight and level flight. It is being acted upon by four forces (shown as vectors, each having a direction as indicated by the arrows and a magnitude expressed here in pounds).
The aerodynamic forces are proportional to the square of airspeed The most fundamental attribute of an airfoil is its "lift-to-drag ratio" ('L/D', pronounced rather hurriedly 'elloverdee') and for a typical single-engine plane, 6 < L/D < 11. Figure 2 provides a horizontal view of an airplane in a left turn, still in level flight. To remain aloft, W must now be balanced by the vertical component of L, which calls for a value of L itself larger than W. The expression "Requisite Lift" gives emphasis to this reality. When b = 0o, cos b = 1 and L = W, as we saw in Figure 1. At any other angle of bank, cos b < 1, which makes L > W. For example, when b = 60o, cos b = 1/2, and L = 2 W. The airplane, along with the passengers inside, "feel" twice as heavy as when they were taxiing for take-off. 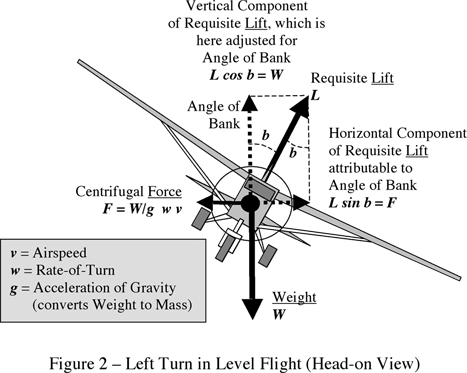 Vectors
can be simplified by strategic selection of vantage
point. Thus,
in Figure 2, neither D nor T
can be "seen"
(T points straight out of your screen, and
D
points straight in). That allows us to exclude D
and
T
in the analysis below. Vectors
can be simplified by strategic selection of vantage
point. Thus,
in Figure 2, neither D nor T
can be "seen"
(T points straight out of your screen, and
D
points straight in). That allows us to exclude D
and
T
in the analysis below.
By inspection of Figure 2, we see that for a turn in level flight, L = W / cos b. Meanwhile, the Lift vector L is manifesting a horizontal component, L sin b, which produces a turning maneuver -- a circular flight path, creating a balancing Centrifugal Force F = L sin b. Sophisticated solvers don't bother to distinguish "centrifugal force" (fugitive from the center of a circular path) and "centripetal acceleration" (that which is capable of drawing a mass toward the center), the equivalence having been settled three centuries ago by Newton's Second Law of Motion. Since L = W / cos b and F = L sin b, then F = W sin b / cos b = W tan b. Since W/g w v = W tan b, the value of W gets canceled out. Solving for rate of turn, we have w = g tan b / v radians per second.
To turn back toward the airport and line up with the runway, the gliding flight path will require more than 180o of turning. As suggested in the sketch, your strategy calls for 270o in one direction (left, say) plus 90o in the opposite direction (right) for a total of 360o of turning, or 2 Fly too slow and the plane stops flying. Oh right, and as b approaches 90o, cos b approaches zero. Look what that does to the requisite Lift. Since L = W / cos b, the force exerted by the wings on the airplane -- and therefore the apparent weight of passengers inside -- will become astronomical.The Pilot's Nightmare puzzle postulates an engine failure during flight. Without propulsion, of course, a plane will be gliding -- but not necessarily diving (movie-makers take note). Figure 3 depicts a horizontal view of an unpowered airplane gliding in a straight line at airspeed v with its Direction of Flight sloping downward at Angle of Descent a. As with v in Figure 1, a is relative to the local parcel of air in which the plane is flying, not necessarily with respect to the ground (with a head-wind equal to v, for example, the plane would be descending vertically). The Pilot's Nightmare puzzle, by the way, assumes landing in a tail-wind, but as shown in Figure 3, the plane has Vertical Descent Rate u = v sin a (in feet per second), where u does not depend on relative wind. Whatever the windspeed, at a given airspeed, the larger the value of a the faster will be the rate of descent u and the sooner the plane will run out of altitude.
As you might expect, there is an optimum airspeed for gliding:
By inspection of Figure 3, then, we see that L = W cos a, and since cos a ? 1, L is less than the aircraft weight W. The previous sentence does not have an exclamation point. It appears instead in the answer to the following question: How can the plane stay aloft if Lift is less than Weight? Aha, there is a vertical component of Drag D that actually helps to hold the airplane up! The casual solver will note in passing that when the Angle of Descent a approaches 90o, cos a approaches zero making Lift totally useless for keeping the plane aloft. Meanwhile, since sin a approaches one, D approaches W, and the plane would be executing a rather steep dive at an airspeed called, somewhat ominously, "terminal velocity."It may not be obvious but if you look closely at Figure 3, you will see that in a power-off glide at v0, the lift-to-drag ratio L/D = cos a / sin a or L/D = 1 / tan a. A gliding plane with an L/D = 10 will therefore have an Angle of Descent a of about 6o. If the plane has a stall speed of, say, 50 nautical miles per hour (kts), minimum drag speed would be about 65 kts (v0 = 110 feet per second). The Vertical Descent Rate calculated as u = v0 sin a will be about 12 feet per second. From 1,000 feet AGL, the pilot would have not quite a minute and a half (83 seconds) before the flight is concluded. Fine, but that assumes no turning.Figure 4 depicts the situation postulated in the Pilot's Nightmare puzzle -- a gliding turn. As in Figure 2, we have made a strategic choice for our vantage point. Our head-on view this time, though, is looking "uphill" along the descending direction of flight. Thus, neither D nor W sin a (the dead-stick replacement for T) can be "seen" in Figure 4.
Gliding, say, at Angle of Descent a = 6o and at an Angle of Bank b = 50o, the requisite Lift L = 1.5 W. The wings are carrying about half again the gross weight of the airplane, which raises the question, how does the pilot increase the value of L? Answer: increase airspeed, of course. But how much?As described above, L increases according as the square of v. To compensate for banking, we observe that the requisite Lift must be increased from its straight-flight value, L = W cos a, by a ratio that looks like this: (W cos a) / (W cos a cos b) or more simply 1 / cos b. Airspeed, then must be increased from its straight-flight value v0 by a ratio that looks like this: v2 / v02. Thus, for a gliding turn, the requisite airspeed will be given by v = v0 (1 / cos b)1/2 (feet per second). Hmm, this determination turns out to be independent of the Angle of Descent a as well as W (a counter-intuitive reality, wouldn't you say?).
Applying simple algebra, we are now able to derive the following two expressions: w = (g / v0 ) (cos a sin b) / (cos b)1/2 (radians per second)Thus, the time to complete the turning maneuver (270o + 90o = 360o = 2 h = 2Here are specifications for my favorite airplane as exemplars for our calculations:
So, then,
using that formula for
h, what angle of bank would
you
choose? The following table gives h
for the values
of b offered in the Pilot's Nightmare
puzzle:
At b = 15o, you will take over 80 seconds to complete your gliding turn and will lose over 900 feet. You can cut that altitude loss almost in half by choosing 30o -- and half again at 60o. Obviously, the greater the value of b, the lesser the value of h. You might as well, therefore, just go ahead and roll your plane on over to a angle of bank. You will complete your maneuver in a little over 11 seconds, with an altitude loss of only feet. Watch out, though... Any maneuver using a bank angle greater than 60o is officially classified as "aerobatic" and can do structural damage to most models of light aircraft. A puzzle-solver might not be expected to know that, perhaps, but it is required knowledge for all pilots -- and for good reason: At a 75o angle of bank, your plane and passengers would be pulling upwards of 4 gs. Your banking stall speed will be 100 kts -- twice that of level flight. The minimum drag speed you must carry will be 130 kts (215.5 feet per second). So maybe you are not about to stall; however, truth be known: The structure of the airframe would actually be less challenged if your plane did stall, thus releasing the "Grasp of Bernouli." A stalled wingfoil therefore makes sure that your airplane will arrive at the crash-site...in one piece.Best check your aircraft owner's manual before horsing around in the sky at a 75o angle of bank. Besides, choosing 60o only costs you 272 feet in altitude loss. Oh, but there's more to think about. Much more...
For our purposes here, let us assume a rather generous roll-rate of 15o per second (for a slowly gliding plane, remember). Rolling the plane from wings level into a bank angle b of, say, 60o for the course reversal will take you about four seconds. The opposite turn requires first rolling the wings level and then rolling into the opposite bank angle to get lined up with the runway -- another eight seconds. Finally, there's rolling the wings level before touch-down, which takes yet another four seconds.
y1 = (b/15)(v + v0 ) / 2, which assumes climbing at minimum drag speed v0 ;The total altitude lost while balancing adverse yaw can be estimated as (y1 + 2y2 + y3) tan a. Figure 5 also
shows cumulative horizontal
heading changes, which turn out (no pun intended) to
be less than the total
of 360o (2 By inspection of Figure 5, we learn that the first turn requires a total of x = 2 (r sinTaking into account the effects of balancing adverse yaw, then, we see in this tabulation...
...that the solution to the Pilot's Nightmare puzzle is b = -- decidedly not b = 75o.
Your altitude at any given point during the climb-out will depend on your Climb Angle c along with the distance flown before engine-failure (the green line). As shown in Figure 6, c better be greater than a or you'll never make it. To determine c, you will need to know your airspeed v and rate of climb u. By the way, wind helps your cause by making your angle of climb steeper and your angle of descent shallower -- and by shortening your take-off roll. However, wind also increases your groundspeed at touch-down. Accordingly,
there are plenty of
technical factors beyond those addresed in solving the
Pilot's
Nightmare puzzle -- factors that may convince
you not to execute the course-reversing
maneuver.
|
| Epilog
The author of the Pilot's Nightmare puzzle does not claim credentials for offering advice to aviators; moreover, the solution above, while drawing upon solid principles, is necessarily incomplete. A multitude of parameters must be considered and calculated for each aircraft, for each airport, for each flight -- all for an eventuality that might not ever arise in a lifetime of flying. Nevertheless, here are a few piloting policies suggested by the solution to the puzzle. While planning each flight, estimate a and c, h and x (see analysis above) for the aircraft, airport, and wind conditions.
2. Always decline a mid-field departure clearance; position the plane for use of the whole runway. 3. Use the Short Field Take-off procedure as specified in the aircraft owners manual (AOM). 4. Always set trim for Best Angle of Climb speed as given in the AOM (see 8 below). 5. Retract landing gear as soon as climb is established. 6. Retract take-off flaps when reaching runway elevation plus h (see 1 above). 7. Scan diligently ahead during climb-out for a suitable emergency landing site (ELS). 8. Upon identifying a suitable ELS (see 7 above) re-trim for Cruise-Climb per AOM.
...between Steps 7 and 8, execute course-reversal maneuver at a 45o angle-of-bank b. ...after Step 8, execute emergency landing at suitable ELS (see 7 above). |